Dependency Injection is a fundamental concept in computer programming. Successfully implemented in many programming languages. What makes it so useful and how .Net Core 3 supports it?
Let’s start with the definition.
Dependency Injection is a software design pattern where dependencies are not created by the client, but rather passed to the client.
In common usage, instead of creating dependencies by new keyword, we will define what we need. We delegate the responsibility of passing those to the injector. Class does not need to know how to create dependency and it’s not a part of its logic.
With a separation of creation and behavior of our service we can build loosely coupled services. In our classes, we concentrate on how it’s going to behave.
This concept, Dependency Injection, is a part of a broader concept – Inversion of Control. Dependency Injection, DI for short, follows two SOLID principles: dependency inversion and single responsibility principle. This concept is crucial for creating well-designed and well-decoupled software, it’s just a must-have.
Why creating dependencies on your own is a bad idea?
var ratingsProvider = new MovieRatingProvider(new MoviesClient("connection"), 3);
- to change implementation of a dependency (in this case MovieRatingProvider), we need to change all places where it is used
- to create dependency we need to create all of its dependencies as well (MoviesClient)
- it’s hard to write unit test – dependencies should be easily mocked. In test we do not want to create MoviesClient, we want to mock it and test MovieRatingProvider
Did you know? There is a way of programming, where you are not allowed to use new keyword outside of the dedicated factory. So you not only delegate creating dependencies to the DI, but also create factories to create all other objects. It’s a good concept, that also not always makes sense.
Practical example
Let’s say we have a Web API for getting events. We have EventsController, that gets events from EventsProvider and it gets movie ratings from MovieRatingProvider. On the schema it will look like this:
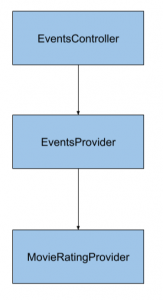
Now lets see the code, EventsController looks like this:
[Route("[controller]")]
[ApiController]
public class EventsController : ControllerBase
{
[HttpGet]
public IActionResult Get()
{
try
{
var provider = new EventProvider();
return new JsonResult(provider.GetActiveEvents());
}
catch (Exception)
{
// logging
return StatusCode(StatusCodes.Status500InternalServerError);
}
}
}
You see that EvenProvider, a dependency, is created by new keyword. Here is how it looks like:
public class EventProvider
{
public IEnumerable<Event> GetActiveEvents()
{
var events = GetAllEvents();
return ApplyRatings(events);
}
private IEnumerable<Event> ApplyRatings(IEnumerable<Event> events)
{
var ratingsProvider = new MovieRatingProvider();
var movieRatings = ratingsProvider.GetMovieRatings(
events.Where(e => e.Type == EventType.Movie)
.Select(m => m.Title));
foreach (var rating in movieRatings)
{
var eventToRate = events.FirstOrDefault(e => e.Title == rating.Key);
if (eventToRate != null)
{
eventToRate.Rating = rating.Value;
}
}
return events;
}
private static IEnumerable<Event> GetAllEvents()
{
// some list here
return Enumerable.Empty<Event>();
}
}
EventProvider is a bit more complicated. It get all events and then for movies it searches for movie ratings and try to apply them. Last dependency – MovieRatingProvider looks like this:
public class MovieRatingProvider
{
public IDictionary<string, decimal> GetMovieRatings(IEnumerable<string> movieTitles)
{
var random = new Random();
var ratings = movieTitles
.Distinct()
.Select(title => new KeyValuePair<string, decimal>(title, (decimal)random.Next(10, 50) / 10));
return new Dictionary<string, decimal> (ratings);
}
}
The first step
What should be the first step to introduce Dependency Injection? Interfaces! We need to introduce interfaces for all our dependencies:
public interface IEventProvider
{
IEnumerable<Event> GetActiveEvents();
}
public interface IMovieRatingProvider
{
IDictionary<string, decimal> GetMovieRatings(IEnumerable<string> movieTitles);
}
And we need to decorate our classes with it:
public class EventProvider : IEventProvider
public class MovieRatingProvider : IMovieRatingProvider
The second step
We need to use our interfaces, instead of concrete classes. How do we do that? We need to pass an interface to our class.
There are two popular ways:
- constructor injection
- property injection
We will use the first one and I think this is a better one because the constructor is the one place that gathers all dependencies together. Let’s see how it looks in EventsController:
[Route("[controller]")]
[ApiController]
public class EventsController : ControllerBase
{
private readonly IEventProvider _eventProvider;
public EventsController(IEventProvider eventProvider)
{
_eventProvider = eventProvider;
}
[HttpGet]
public IActionResult Get()
{
try
{
return new JsonResult(_eventProvider.GetActiveEvents());
}
catch (Exception)
{
// logging
return StatusCode(StatusCodes.Status500InternalServerError);
}
}
}
We are passing IEventProvider in the constructor and save it as private property. It will not be available outside of that class, but you will be able to use the same instance of EventProvider in every method of your class, brilliant!
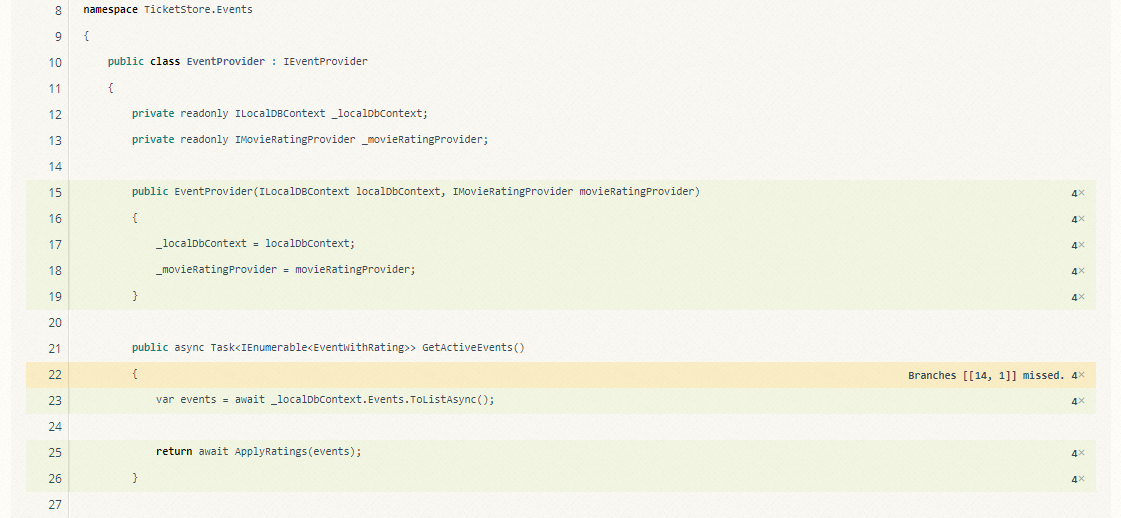
Now let’s look at the EventProvider:
public class EventProvider : IEventProvider
{
private readonly IMovieRatingProvider _movieRatingProvider;
public EventProvider(IMovieRatingProvider movieRatingProvider)
{
_movieRatingProvider = movieRatingProvider;
}
public IEnumerable<Event> GetActiveEvents()
{
var events = GetAllEvents();
return ApplyRatings(events);
}
private IEnumerable<Event> ApplyRatings(IEnumerable<Event> events)
{
var movieRatings = _movieRatingProvider.GetMovieRatings(
events.Where(e => e.Type == EventType.Movie)
.Select(m => m.Title));
foreach (var rating in movieRatings)
{
var eventToRate = events.FirstOrDefault(e => e.Title == rating.Key);
if (eventToRate != null)
{
eventToRate.Rating = rating.Value;
}
}
return events;
}
private static IEnumerable<Event> GetAllEvents()
{
// some list here
return Enumerable.Empty<Event>();
}
}
An implementation of IMovieRatingProvider is also passed with constructor injection and saved in a private property. All is ready for…
The Final step
In .Net Core 3 support for Dependency Injection is built-in into the framework, therefore, you don’t need to do much to make it work. All you need to do is to go to Startup class and in ConfigureServices method, add registrations of your services.
public void ConfigureServices(IServiceCollection services)
{
services.AddControllers();
services.AddScoped<IMovieRatingProvider, MovieRatingProvider>();
services.AddScoped<IEventProvider, EventProvider>();
}
I added services.AddScoped methods, that bind an interface to the class that we implement. This is how the framework knows what instance of a class passes when you define your dependency with an interface. Simple as that, those where all of the changes that needed to be introduced to make it work. Let’s see the new application schema side by side with the old one:
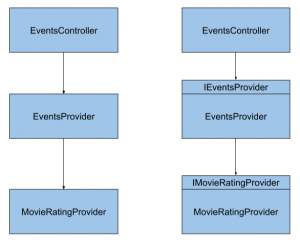
Single point of configuration
The Startup class and ConfigureServices method is the only place where we need to put configuration for the whole application. Even if you are using multiple projects, you will need to configure DI only once in Startup class. This applies for a single executable project, like Web API or ASP.Net website. If you have two projects like this in your solution, you would need to configure DI in both of them.
Service lifetimes
You probably noticed that I used AddScoped method to register my dependencies. This is one of the three service lifetimes that you can use:
- Transient (AddTransient)
- Scoped (AddScoped)
- Singleton (AddSingleton)
Those service lifetimes are pretty standard for any Dependency Injection container. Let’s have a quick look at what they are for.
Scoped lifetime – the most popular one. If you register your services as scoped, it will be created only once per request. It means, that whenever you use the same interface representing your dependency, the same instance will be returned within one request. Let’s have a look at this simple example:
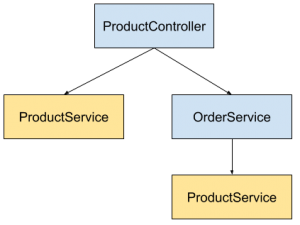
Here when ProductController is called, it depends on ProductService and OrderService, which also depends on ProductService. In this case .Net Core 3 DI will resolve ProductService dependency twice, but it will create ProductService once and return the same object in both places. This will happen in scoped lifetime, because it is the same request. In most cases, you should be using this one.
Transient lifetime – if you register your service with a transient lifetime, you will get a new object whenever you fetch it as a dependency, no matter if it is a new request or the same one
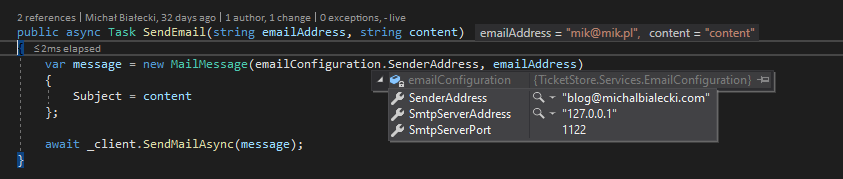
Singleton lifetime – this is the most tricky one. Singleton is a design pattern that is very well known. In this pattern whenever you use an object, you will get the same instance of it, every time, even in a different request or a different thread. This is an invitation to problems and this is also why it is called an antipattern sometimes. With singleton lifetime you will get the same instance of your object every time, for the whole lifetime of your application. It’s not a bad idea to use singleton, but you need to implement it in a thread-sefe manner. It may be useful whenever the creation of an object is expensive (time or resource-wise) and you would rather keep it in memory for the next usage, then creating it every time. For example, you can use a singleton to create a service to send an email. Creating SmtpClient is expensive and can be done only once.
public class EmailSenderService : IEmailSenderService
{
private readonly IConfiguration _configuration;
private readonly SmtpClient _client;
public EmailSenderService(IConfiguration configuration)
{
_configuration = configuration;
var smtpServerAddress = _configuration.GetValue<string>("Email:smtpServerAddress");
var smtpServerPort = _configuration.GetValue<int>("Email:smtpServerPort");
_client = new SmtpClient(smtpServerAddress, smtpServerPort);
}
public async Task SendEmail(string emailAddress, string content)
{
var fromAddress = _configuration.GetValue<string>("Email:senderAddress");
var message = new MailMessage(fromAddress, emailAddress);
message.Subject = content;
await _client.SendMailAsync(message);
}
}
And in Startup class:
services.AddSingleton<IEmailSenderService, EmailSenderService>();
Is built-in DI container enough?
This is an important question to ask. Microsoft did a great job in developing a Dependency Injection container, but there are several great solutions out there that are ready to use. Actually, Microsoft lists them on an official documentation page: https://docs.microsoft.com/en-gb/aspnet/core/fundamentals/dependency-injection?view=aspnetcore-3.1#default-service-container-replacement
So what are popular DI containers you might try out?
And those are only a few, there are more. The important thing is how they are different from a built-in container. The obvious answer is that they offer more. So what Microsofts built-in container doesn’t offer?
- property injection
- custom lifetime management
- lazy initialization
- auto initialization based on name
I must admit, that I miss the last one the most. In SimpleInjector for .Net Core 2.1 it was possible to register dependencies if only they follow naming convention with an interface having the same name as implementing class, with preceding ‘I’. There was no need to write registration for 90% of cases.
So what I would use?
I would use a built-in container, whenever I don’t need any specific features. Without 3rd party nuget packages code is cleaner and easier to understand. .Net Core 3 doest pretty good job and you probably won’t need anything else.
Hope you enjoyed this post, you can have a look at the code posted here on my Github:

https://github.com/mikuam/TicketStore