 Microsoft Orleans is a developer-friendly framework for building distributed, high-scale computing applications. It does not require from developer to implement concurrency and data storage model. It requires developer to use predefined code blocks and enforces application to be build in a certain way. As a result Microsoft Orleans empowers developer with a framework with an exceptional performance.
Microsoft Orleans is a developer-friendly framework for building distributed, high-scale computing applications. It does not require from developer to implement concurrency and data storage model. It requires developer to use predefined code blocks and enforces application to be build in a certain way. As a result Microsoft Orleans empowers developer with a framework with an exceptional performance.
Orleans proved its strengths in many scenarios, where the most recognizable ones are cloud services for Halo 4 and 5 games.
You can have a look at full introduction in my previous post: Getting started with Microsoft Orleans
The Scenario
To test the performance of Microsoft Orleans I’ll compare it to simple micro-service implementation. The scenario is about transferring money from one account to another using a persistent storage. Here is the idea:
- Both services will use .Net Core
- Data will be saved in Azure CosmosDB database
- Services will read and send messages from Service Bus
- One message will trigger transferring money, that will need to get and save data from DB and then service will send two messages with account balance updates
Simple Micro-service approach
This app is really simple. It is a console application, that registers message handler and processes messages. This is how architecture looks like, simple right?
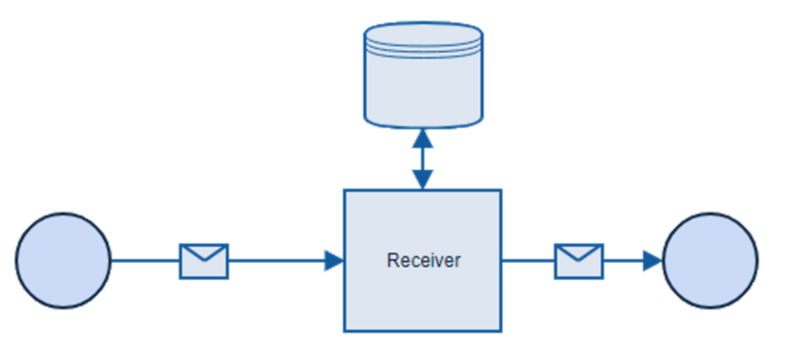
Code that handles message looks like this:
public void Run()
{
var service = new TableStorageService(_configuration);
try
{
var subscriptionClient = new SubscriptionClient(
_configuration[ServiceBusKey],
"accountTransferUpdates",
"commonSubscription");
subscriptionClient.PrefetchCount = 1000;
subscriptionClient.RegisterMessageHandler(
async (message, token) =>
{
var messageJson = Encoding.UTF8.GetString(message.Body);
var updateMessage = JsonConvert.DeserializeObject<AccountTransferMessage>(messageJson);
await service.UpdateAccount(updateMessage.From, -updateMessage.Amount);
await service.UpdateAccount(updateMessage.To, updateMessage.Amount);
Console.WriteLine($"Processed a message from {updateMessage.From} to {updateMessage.To}");
},
new MessageHandlerOptions(OnException)
{
MaxAutoRenewDuration = TimeSpan.FromMinutes(60),
MaxConcurrentCalls = 1,
AutoComplete = true
});
}
catch (Exception e)
{
Console.WriteLine("Exception: " + e.Message);
}
}
private Task OnException(ExceptionReceivedEventArgs args)
{
Console.WriteLine(args.Exception);
return Task.CompletedTask;
}
TableStorageService is used to synchronize state with the database, which in this case it read and update account balance.
public class TableStorageService
{
private const string EndpointUriKey = "CosmosDbEndpointUri";
private const string PrimaryKeyKey = "CosmosDbPrimaryKey";
private const string ServiceBusKey = "ServiceBusConnectionString";
private readonly DocumentClient client;
private readonly TopicClient topic;
public TableStorageService(IConfigurationRoot configuration)
{
client = new DocumentClient(new Uri(configuration[EndpointUriKey]), configuration[PrimaryKeyKey]);
topic = new TopicClient(configuration[ServiceBusKey], "balanceUpdates");
}
public async Task UpdateAccount(int accountNumber, decimal amount)
{
Account document;
try
{
var response = await client.ReadDocumentAsync<Account>(accountNumber.ToString());
document = response.Document;
document.Balance += amount;
await client.ReplaceDocumentAsync(accountNumber.ToString(), document);
}
catch (DocumentClientException de)
{
if (de.StatusCode == HttpStatusCode.NotFound)
{
document = new Account { Id = accountNumber.ToString(), Balance = amount };
await client.CreateDocumentAsync(UriFactory.CreateDocumentCollectionUri("bialecki", "accounts"), document);
}
else
{
throw;
}
}
await NotifyBalanceUpdate(accountNumber, document.Balance);
}
private async Task NotifyBalanceUpdate(int accountNumber, decimal balance)
{
var balanceUpdate = new BalanceUpdateMessage
{
AccountNumber = accountNumber,
Balance = balance
};
var message = new Message(Encoding.UTF8.GetBytes(JsonConvert.SerializeObject(balanceUpdate)));
await topic.SendAsync(message);
}
}
DocumentClient is CosmosDB client provided by the framework. You might be intrigued by try-catch clause. Currently for in CosmosDB package for .Net Core there is no way to check if the document exists and the proposed solution is to handle an exception when the document is not found. In this case, the new document will be created. NotifyBalanceUpdate sends messages to Service Bus.
When we go to Azure portal, we can query the data to check if it is really there:
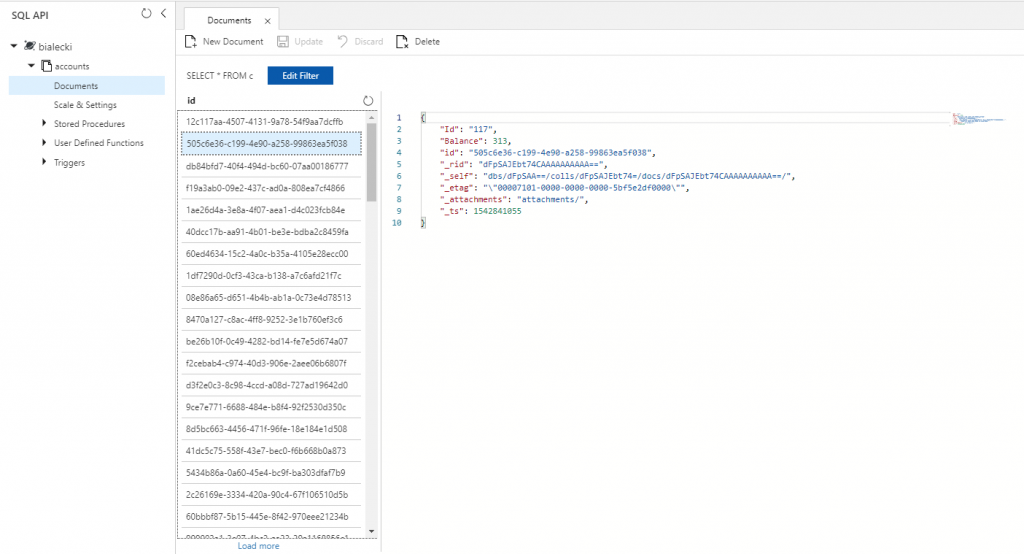
This is how reading 100 messages looks like:
Microsoft Orleans approach
Microsoft Orleans is an actor framework, where each actor can be understood as a separate service, that does some simple operations and can have its own state. In this case, every account can be an actor, it doesn’t matter if we have few or few hundred thousands of them, the framework will handle that. Another big advantage is that we do not need to care about concurrency and persistence, it is also handled by the framework for us. In Orleans, accounts can perform operations in parallel. In this case, the architecture looks much different.
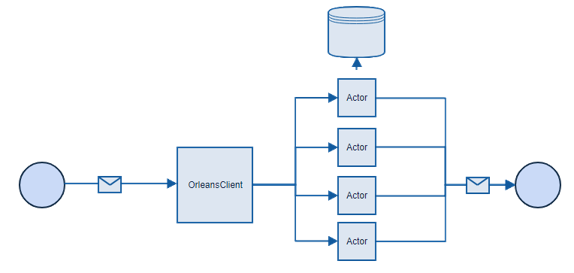
Project structure looks like this:
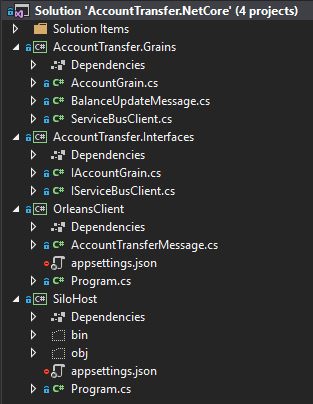
- SiloHost – sets up and run a silo to host grains, which is just another name for actors
- OrleansClient – second application. This one connects to the silo and run client code to use grains
- AccountTransfer.Interfaces – its an abstraction for grains
- AccountTransfer.Grains – grains implementation, that handles business logic
Let’s have a look at how running a silo looks like:
public class Program
{
private static IConfigurationRoot configuration;
public static int Main(string[] args)
{
return RunMainAsync().Result;
}
private static async Task<int> RunMainAsync()
{
try
{
var builder = new ConfigurationBuilder()
.SetBasePath(Directory.GetCurrentDirectory())
.AddJsonFile("appsettings.json", optional: true, reloadOnChange: true);
configuration = builder.Build();
var host = await StartSilo();
Console.WriteLine("Press Enter to terminate...");
Console.ReadLine();
await host.StopAsync();
return 0;
}
catch (Exception ex)
{
Console.WriteLine(ex);
return 1;
}
}
private static async Task<ISiloHost> StartSilo()
{
var builder = new SiloHostBuilder()
.UseLocalhostClustering()
.Configure<EndpointOptions>(options => options.AdvertisedIPAddress = IPAddress.Loopback)
.ConfigureServices(context => ConfigureDI(context))
.ConfigureLogging(logging => logging.AddConsole())
.UseInClusterTransactionManager()
.UseInMemoryTransactionLog()
.AddAzureTableGrainStorageAsDefault(
(options) =>
{
options.ConnectionString = configuration.GetConnectionString("CosmosBDConnectionString");
options.UseJson = true;
})
.UseTransactionalState();
var host = builder.Build();
await host.StartAsync();
return host;
}
private static IServiceProvider ConfigureDI(IServiceCollection services)
{
services.AddSingleton<IServiceBusClient>((sp) => new ServiceBusClient(configuration.GetConnectionString("ServiceBusConnectionString")));
return services.BuildServiceProvider();
}
}
This is the whole code. Amazingly short comparing to what we are doing here. Notice, that configuring CosmosDB Azure Table storage takes just a few lines. I even configured dependency injection that I will use in account grain.
This is how connecting to silo looks like:
public class Program
{
private static IConfigurationRoot configuration;
static int Main(string[] args)
{
return RunMainAsync().Result;
}
private static async Task<int> RunMainAsync()
{
try
{
var builder = new ConfigurationBuilder()
.SetBasePath(Directory.GetCurrentDirectory())
.AddJsonFile("appsettings.json", optional: true, reloadOnChange: true);
configuration = builder.Build();
using (var client = await StartClientWithRetries())
{
DoClientWork(client);
Console.ReadKey();
}
return 0;
}
catch (Exception e)
{
Console.WriteLine(e);
return 1;
}
}
private static async Task<IClusterClient> StartClientWithRetries(int initializeAttemptsBeforeFailing = 5)
{
int attempt = 0;
IClusterClient client;
while (true)
{
try
{
client = new ClientBuilder()
.UseLocalhostClustering()
.Configure<ClusterOptions>(options =>
{
options.ClusterId = "dev";
options.ServiceId = "AccountTransferApp";
})
.ConfigureApplicationParts(parts => parts.AddApplicationPart(typeof(IAccountGrain).Assembly).WithReferences())
.ConfigureLogging(logging => logging.AddConsole())
.Build();
await client.Connect();
Console.WriteLine("Client successfully connect to silo host");
break;
}
catch (SiloUnavailableException)
{
attempt++;
Console.WriteLine($"Attempt {attempt} of {initializeAttemptsBeforeFailing} failed to initialize the Orleans client.");
if (attempt > initializeAttemptsBeforeFailing)
{
throw;
}
await Task.Delay(TimeSpan.FromSeconds(4));
}
}
return client;
}
private static Task HandleException(ExceptionReceivedEventArgs args)
{
Console.WriteLine(args.Exception + ", stack trace: " + args.Exception.StackTrace);
return Task.CompletedTask;
}
}
This is also a simple console application. Both apps need to be run together, cause client is connecting to the silo and if fails, tries again after few seconds. The only part missing here is DoClientWork method:
private static void DoClientWork(IClusterClient client)
{
var subscriptionClient = new SubscriptionClient(
configuration.GetConnectionString("ServiceBusConnectionString"),
"accountTransferUpdates",
"orleansSubscription",
ReceiveMode.ReceiveAndDelete);
subscriptionClient.PrefetchCount = 1000;
try
{
subscriptionClient.RegisterMessageHandler(
async (message, token) =>
{
var messageJson = Encoding.UTF8.GetString(message.Body);
var updateMessage = JsonConvert.DeserializeObject<AccountTransferMessage>(messageJson);
await client.GetGrain<IAccountGrain>(updateMessage.From).Withdraw(updateMessage.Amount);
await client.GetGrain<IAccountGrain>(updateMessage.To).Deposit(updateMessage.Amount);
Console.WriteLine($"Processed a message from {updateMessage.From} to {updateMessage.To}");
await Task.CompletedTask;
},
new MessageHandlerOptions(HandleException)
{
MaxAutoRenewDuration = TimeSpan.FromMinutes(60),
MaxConcurrentCalls = 20,
AutoComplete = true
});
}
catch (Exception e)
{
Console.WriteLine("Exception: " + e.Message);
}
}
This is almost the same code that we had in micro-service approach. We are reading Service Bus messages and deserialize them, but then we use actors. From this point execution will be handled by them. AccountGrain looks like this:
[Serializable]
public class Balance
{
public decimal Value { get; set; } = 1000;
}
public class AccountGrain : Grain<Balance>, IAccountGrain
{
private readonly IServiceBusClient serviceBusClient;
public AccountGrain(
IServiceBusClient serviceBusClient)
{
this.serviceBusClient = serviceBusClient;
}
async Task IAccountGrain.Deposit(decimal amount)
{
try
{
this.State.Value += amount;
await this.WriteStateAsync();
await NotifyBalanceUpdate();
}
catch (Exception e)
{
Console.WriteLine(e);
}
}
async Task IAccountGrain.Withdraw(decimal amount)
{
this.State.Value -= amount;
await this.WriteStateAsync();
await NotifyBalanceUpdate();
}
Task<decimal> IAccountGrain.GetBalance()
{
return Task.FromResult(this.State.Value);
}
private async Task NotifyBalanceUpdate()
{
var balanceUpdate = new BalanceUpdateMessage
{
AccountNumber = (int)this.GetPrimaryKeyLong(),
Balance = this.State.Value
};
var message = new Message(Encoding.UTF8.GetBytes(JsonConvert.SerializeObject(balanceUpdate)));
await serviceBusClient.SendMessageAsync(message);
}
}
Notice that on top we have serializable Balance class. When defining actor like this: AccountGrain : Grain<Balance>, it means that Balance will be our state, that we can later refer to as this.State. Getting and updating state is trivial, and both Withdraw and Deposit causes sending Service Bus message by calling NotifyBalanceUpdate.
In Azure portal we can have a look how data is saved. I choose to serialize it to json, so we can see account state easily:
Let’s have a look at reading 1000 messages by a single thread with Microsoft Orleans looks like:
It runs noticeably faster, but what’s more interesting is that we can read messages with even 20 concurrent threads at a time:
Comparsion
As you could see, I used two approaches to read and process 100 and 1000 Service Bus messages, written in .net core with a persistant state in remote CosmosDB database. Results can be seen here:
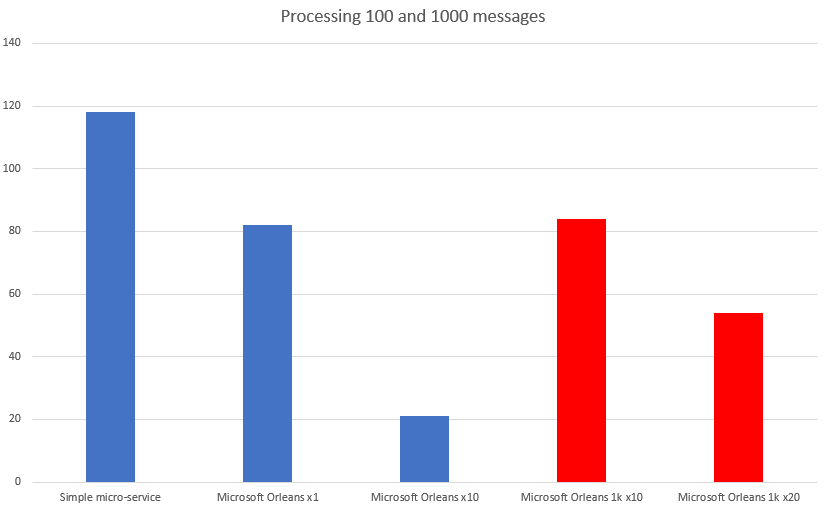
Blue color represents reading 100 messages, red represents reading 1000 messages. As you can see Microsoft Orleans is a few times faster.
To sum up, using Microsoft Orleans:
Pros:
- Microsoft actor framework could give you outstanding performance
- It requires minimal knowledge to write your first app
- Documentation is great
- The code is open source, you can post issues
Cons:
- It doesn’t fit every scenario
- Maintenance and deployment is a bit more difficult than a simple IIS app
If you’re interested in the code, have a look at my GitHub:
- micro-service approach: https://github.com/mikuam/Blog/
- Microsoft Orleans approach: https://github.com/mikuam/orleans-core-example
Pingback: dotnetomaniak.pl
What’s the y-axis on your graph?
Those are seconds. But bear in mind, that it is a local machine config and on a server, it could be much less.
SiloHost miss json file.