Would you like to learn how to write programs in .NET and find out what the platform from Microsoft can do? What tools to use and where to start? You’ve come to the right place! I will explain everything step by step.
What is .NET?
.NET is a programming platform created by Microsoft. Here are the most important features:
- You can write in many languages: C #, F # and VB.NET
- libraries written in different languages in .NET can work together because they are compiled into IL intermediate code
- .NET 5 and associated technologies are open and their sources are available on the GitHub platform
- in .NET 5 you can build console applications, websites, APIs, games, mobile applications and desktop computers
- .NET is extremely popular, therefore it has many ready integrations with Amazon or Google technologies, but the easiest way will be to work with Microsoft products and the Azure cloud
- the program written in .NET 5 can be easily run on Windows, Linux and MacOS
Of course, these few points in no way exhaust the topic, because you could easily write a few books what .NET is capable of, but at the beginning it’s a quick summary is enough.
What do I need to install?
To build applications you need to install the development tools package, i.e. the SDK. To run them – the development package.
You’ll find both here: https://dotnet.microsoft.com/download/dotnet/5.0
When choosing the Runtime, choose the one that you need:
- ASP.NET Core – for building a web application
- Desktop – for building Windows-based desktop applications
- .NET Runtime – for building console applications
One of the above is enough to start with. I would recommend ASP.NET Core.
What to write programs with?
Apparently, a good programmer will cope with a notepad, but I think this era is long over. There are actually two good options to choose from.
Visual Studio
A huge and very popular code editor. It is a real multi-tool, it is perfectly integrated with all Microsoft technologies, especially the older ones. I use it for many years and I can’t imagine working without it.
The most important features:
- convenient editor, where many things can be done from UI
- support for older Microsoft technologies
- available on Windows and MacOS
- paid, however, there is a free, stripped-down version – Community
Visual Studio Code
Simple, cross-platform code editor, developed open-source. It does not have as many integrations as Visual Studio, but it is lightweight and thanks to free extensions, it can be easily adapted to your needs. Certainly, however, it works comfortably with smaller projects and with websites. I use it when I’m working with React.js, for example.
The most important features:
- is fast and light
- it’s free and it’s easy to customize
- works under Windows, Linux and MacOS
- integration with older Microsoft technologies is not the best, but with .NET Core and .NET 5 it works great
And any other actually
Because .NET 5 comes with CLI we can create, build and run the project, and also execute tests with simple console commands. For writing code, any editor will do and some of my peers choose to use JetBrain Rider. It is a great, cross-platform IDE, that has a built-in Resharper. It’s also fast and intuitive, so the choice is yours.

Your first app
The wizard in Visual Studio
The easiest way to create your first program in .NET 5 is to use one of the ready-made programs in Visual Studio. This environment offers us many options to choose from:
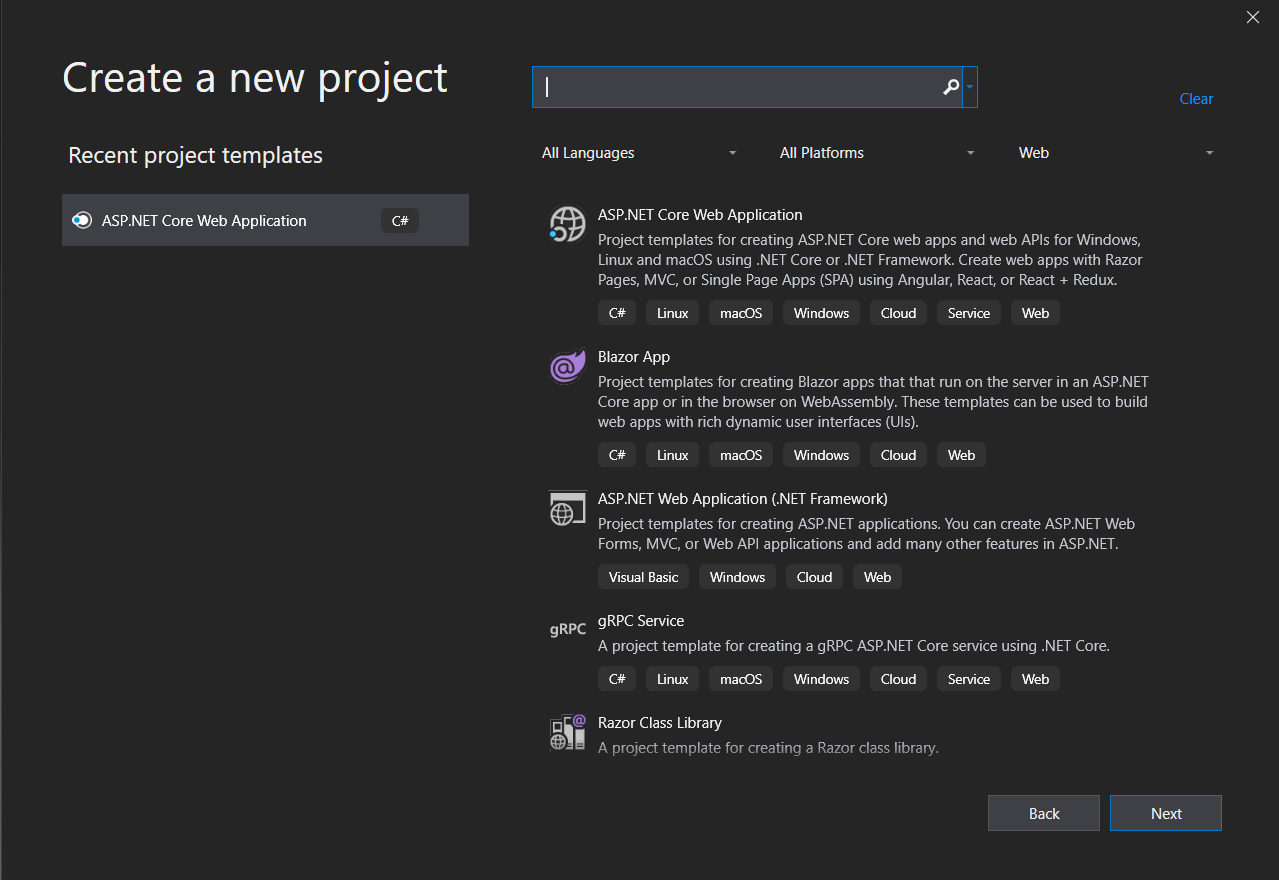
The simplest project that you can choose to start with is the console application in C #. However, if you prefer to start with a web project, select ASP.NET Core application.
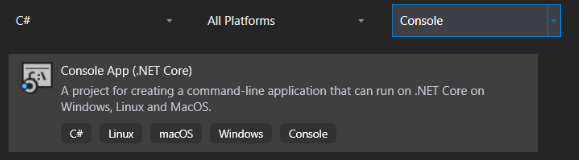
To make sure you’re using .NET 5, edit the project file and check what value is entered in the TargetFramework should be net5.0.
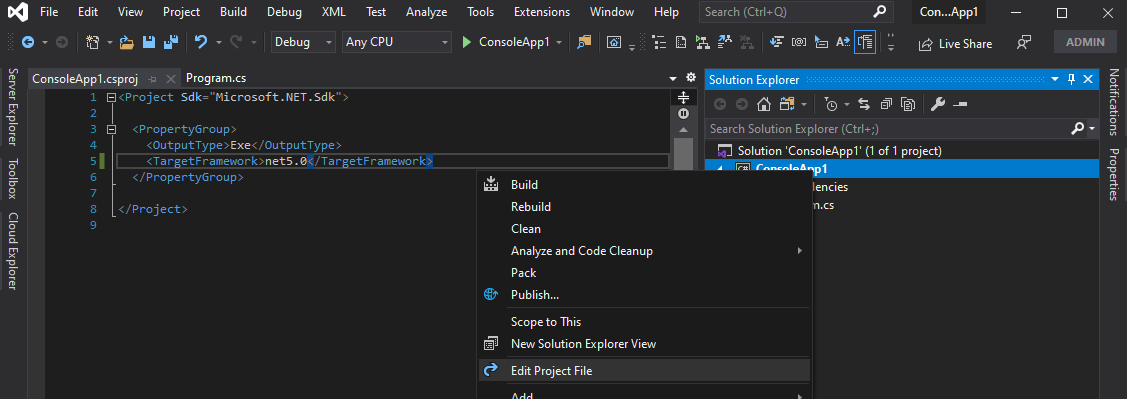
To start the project, simply press F5. At this point, the console application will start and a black window will appear saying Hello World!.
New project in Visual Studio Code
.NET Core and .NET 5 are released together with .NET CLI, a cross-platform set of commands that allows you to create, build, and publish .NET projects. Cross-platform is an important word here – it is thanks to CLI that we can build and run programs in .NET 5 not only on Windows but also on Linux and MacOS.
Let’s create a new project. When we open Visual Studio Code, open a new terminal and enter the dotnet new --list command to see what projects are currently available.
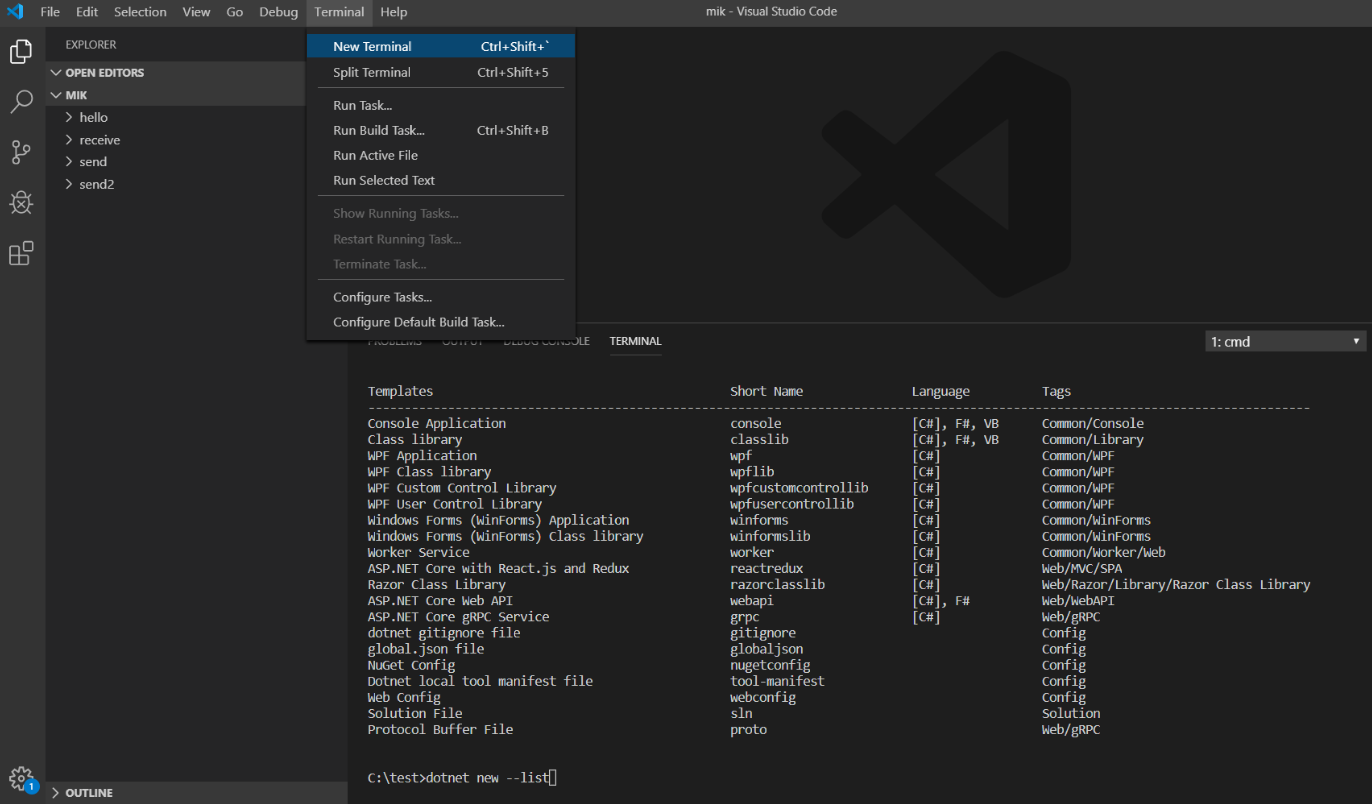
To create a console application called ConsoleApp2, type dotnet new console -n ConsoleApp2.
Great, we already have a console application with a single C# file called Program.cs. We need to know two more commands:
dotnet build– to build the appdotnet run– to run the app
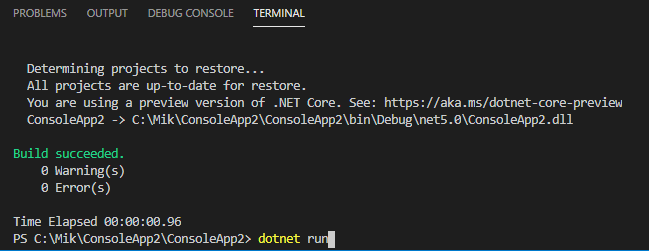
After a few seconds, your eyes will see a black window with the program.
The summary
Programming in .NET 5 can start very quickly and after a while writing your own programs. In addition, they will work not only on Windows but also on Linux and MacOS. They can also operate in the cloud, e.g. in containers. The possibilities are really huge.
If you would like to learn more about programming in the console, take a look at the series of my articles: How to make you console app look cool
If you’re starting your adventure with .NET, you’ve come to the right place. Subscribe to my blog and get information about new posts – you will definitely learn something interesting from them.
Cheers and good luck 🙂

Is the target not net5.0?
net5.0 not netcoreapp5.0 as of the latest preview.
Yes, that’s correct! From preview 2 to preview 4 Target Framework Moniker changed to net5.0. Good article about it can be found here: https://www.thomasclaudiushuber.com/2020/03/26/net-5-merging-net-core-and-net-standard-with-new-target-framework-monikers-tfms/
Great article, but why so microsoft-centric?
Many architects succesfully deploy .net solutions in AWS and GCP. Alternative editors exist, such as Sublime (with omnisharp), Jetbrains Rider, …
There is a .Net world outside Microsoft too…
Agree, there’s more than Microsoft solutions!
It is due to my experience, cause I always worked with Visual Studio. I’m more comfortable with writing something I know. Thanks for sharing!
I’d like to echo Jer0enh’s comment.
With one of the big selling points of .NET Core being its cross-platform support, it’s unfortunate that this post focuses so much on the Windows options and doesn’t call out options for anyone using Mac/Linux by at least acknowledging cross-platform alternatives like Rider (heck, it’s amazing on Windows too!).
Even if you’ve not used it before I still feel it’d be valuable to anyone new to the ecosystem to know it exist and stops Mac/Linux reads feel excluded.
Perhaps those who complain about the MS-centric presentation can invest the time and energy and create their own Mac/Linux material.
Hello, great article thank you ;).
according to the following article
https://devblogs.microsoft.com/vbteam/visual-basic-support-planned-for-net-5-0/comment-page-1/#comment-299
it was expected that vb.net would be supported to make web api in .net5. but I do not find the possibility of doing it.
Obviously I prefer the C # but for a big application already in production I would like to keep the vb.net.
i can’t make a new web api project in .net 5 using vb.net
Do you have any idea how to do this?
thank’s 😉
great article. keep the good work of posting useful material about .net programming.
Pingback: Создание первого приложения на .NET 5.0 в Visual Studio Code для ARM - DevDotNet.ORG
Nice! It’s worth mentioning .NET 5 (and newer) gives you also new C# language features. To use them in libraries we can (and probably should) multi target them to .NET Standard 2.0 and .NET 5.0. For me the greatest feature of .NET 5.0 is I can do code intended for both Windows and Linux, using OS dependent features that are determined at runtime. Anyway – everything in code, that is mostly compatible. I’m just rewriting my Windows services, man, this is way easier and simpler in .NET 5.0! What’s more, the code has a huge chance to be run on Linux server without many changes!
So, wait. You install Visual Studio Code but all you do with it is launch a terminal to run command line commands for creating new projects and building them? Why can’t you do that from the IDE you just installed?
I am trying to learn C# but Visual Studio (Community version) is of little help. I like to use the console command, csc, because it gives me much greater control and, consequently, more learning capabilities. Unfortunately, I haven’t found a way to incorporate .NET 5.0 into this scenario. I want to use SQLite database management system but it requires .NET 5.0. Any suggestions on how to go about achieving this? Thank you.
You can use SQLite in .Net Core 3.1, if you don’t want to use .NET 5. Using EF Core in this case is all the same, apart from configuration of a provider. Take a look at this article: https://kontext.tech/column/dotnet_framework/275/sqlite-in-net-core-with-entity-framework-core